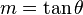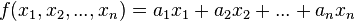Matemáticas: 2013

martes, 15 de enero de 2013

FUNCIONES CUADRATICAS

Definición

Una función cuadrática es aquella que puede escribirse de la forma:

f(x) = ax² + bx + c

donde a, b y c son números reales cualesquiera y a distinto de cero.

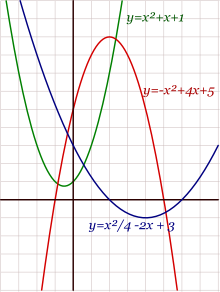
Si representamos "todos" los puntos (x,f(x)) de una función cuadrática, obtenemos siempre una curva llamada parábola.

Obtención del vértice de una parábola

El vértice de una parábola está situado en el eje de ésta y, por tanto, su abscisa será el punto medio de las abscisas de dos puntos de la parábola que sean simétricos.
Como toda función cuadrática pasa por el punto (0,c) y el simétrico de éste tiene de abscisa x = -b/a, la del vértice será Xv = -b/2a. La ordenada Yv se calcula sustituyendo el valor de Xv en la ecuación de la función.

En matemáticas, una función cuadrática o función de segundo grado es una función polinómica definida como:

Gráficas de funciones cuadráticas.

$f(x) = ax^2 + bx + c \,$

en donde a, b y c son números reales (constantes) y a es distinto de 0.

La representación gráfica en el plano cartesiano de una función cuadrática es una parábola, cuyo eje de simetría es paralelo al eje de las ordenadas. La parábola se abrirá hacia arriba si el signo de a es positivo, y hacia abajo en caso contrario. El estudio de las funciones cuadráticas tiene numerosas aplicaciones en campos muy diversos, como por ejemplo lacaída libre o el tiro parabólico.

La derivada de una función cuadrática es una función lineal y su integral una función cúbica.

Representación analítica

Existen tres formas principales de escribir una función cuadrática, aplicables según el uso que se le quiera dar a la función: un estudio analítico de la función o de la ecuación cuadrática, una interpretación o construcción geométrica de la parábola, etc. Las tres formas son equivalentes.

Forma desarrollada

La forma desarrollada de una función cuadrática (o forma estándar) corresponde a la del polinomio de segundo grado, escrito convencionalmente como:

$f(x) = ax^2 + bx + c \,$

con $a \neq 0$ .

Forma factorizada

Toda función cuadrática se puede escribir en forma factorizada en función de sus raíces como:

$f(x) = a(x - x_1)(x - x_2) \,$

siendo a el coeficiente principal de la función, y $x_1$ y $x_2$ las raíces de $f(x)$ . En el caso de que el discriminante Δ sea igual a 0 entonces $x_1 = x_2$ por lo que la factorización adquiere la forma:

$f(x) = a(x - x_1)^2 \,$

En este caso a $x_1$ se la denomina raíz doble, ya que su orden de multiplicidad es 2.

Forma canónica

Toda función cuadrática puede ser expresada mediante el cuadrado de un binomio de la siguiente manera:

$f(x) = a (x - h)^2 + k \,$

siendo a el coeficiente principal y el par ordenado (h;k) las coordenadas del vértice de la parábola.

Determinar la ecuación conocidos tres puntos

Partiendo de la forma de la ecuación:

$y = ax^2 +bx +c \,$

y conocidos tres puntos del plano xy por los que pasa una función polinómica de segundo grado:

$(x_1,y_1), \; (x_2,y_2), \; (x_3,y_3)$

se cumplira que:

$\left \{ \begin{matrix} y_1 = ax_{1}^2 +bx_1 +c \\ y_2 = ax_{2}^2 +bx_2 +c \\ y_3 = ax_{3}^2 +bx_3 +c \end{matrix} \right .$

con lo que tenemos un sistema de tres ecuaciones con tres incógnitas, donde las incógnitas son: a, b y c, este sistema tendrá solución si el determinante de los coeficientes de las incógnitas es distinto de cero.

Representando el sistema ordenado de forma convencional:

$\left \{ \begin{matrix} ax_{1}^2 +bx_1 +c = y_1 \\ ax_{2}^2 +bx_2 +c = y_2 \\ ax_{3}^2 +bx_3 +c = y_3 \end{matrix} \right .$

Con lo que podemos calcular los valores de los coeficientes:

$a = \cfrac{ \left | \begin{matrix} y_1 & x_1 & 1 \\ y_2 & x_2 & 1 \\ y_3 & x_3 & 1 \end{matrix} \right | }{ \left | \begin{matrix} x_{1}^2 & x_1 & 1 \\ x_{2}^2 & x_2 & 1 \\ x_{3}^2 & x_3 & 1 \end{matrix} \right | }$

$, \quad b = \cfrac{ \left | \begin{matrix} x_{1}^2 & y_1 & 1 \\ x_{2}^2 & y_2 & 1 \\ x_{3}^2 & y_3 & 1 \end{matrix} \right | }{ \left | \begin{matrix} x_{1}^2 & x_1 & 1 \\ x_{2}^2 & x_2 & 1 \\ x_{3}^2 & x_3 & 1 \end{matrix} \right | }$

$, \quad c = \cfrac{ \left | \begin{matrix} x_{1}^2 & x_1 & y_1 \\ x_{2}^2 & x_2 & y_2 \\ x_{3}^2 & x_3 & y_3 \end{matrix} \right | }{ \left | \begin{matrix} x_{1}^2 & x_1 & 1 \\ x_{2}^2 & x_2 & 1 \\ x_{3}^2 & x_3 & 1 \end{matrix} \right | }$

A CONTINUACION TE PRESENTAMOS UN VÍDEO EN LA CUAL PUEDES OBSERVAR COMO RESOLVER FUNCIONES

CUADRÁTICAS

VALOR ABSOLUTO

En matemática, el valor absoluto o módulo¹ de un número real es su valor numérico sin tener en cuenta su signo, sea este positivo (+) o negativo (-). Así, por ejemplo, 3 es el valor absoluto de 3 y de -3.

El valor absoluto está relacionado con las nociones de magnitud, distancia y norma en diferentes contextos matemáticos y físicos. El concepto de valor absoluto de un número real puede generalizarse a muchos otros objetos matemáticos, como son los cuaterniones,anillos ordenados, cuerpos o espacios vectoriales.

Características

La imagen de una función valor absoluto es positiva. Para representarla hay que descomponerla.

§ Ponemos delante de una función un signo + y uno negativo, obtenemos una función definida a trozos.

§ La función cambia en aquellos valores donde se anula la X de la función valor absoluto.

§ Para poner las zonas de cada una tenemos en cuenta la función siempre es positiva.

§ Damos valores a cada uno de los trozos para representarla.

Valor absoluto de un número real

Formalmente, el valor absoluto o módulo de todo número real está definido por:2 ejemplos básicos:

Note que, por definición, el valor absoluto de siempre será mayor o igual que cero y nunca negativo. Desde un punto de vista geométrico, el valor absoluto de un número real es siempre positivo o cero, pero nunca negativo. En general, el valor absoluto de la diferencia de dos números reales es la distancia entre ellos. De hecho, el concepto de función distancia o métrica en matemáticas se puede ver como una generalización del valor absoluto de la diferencia, a la distancia a lo largo de la recta numérica real

Otras propiedades

A CONTINUACION TE PRESENTAMOS LA FORMA DE COMO RESOLVER FUNCIONES CON VALOR ABSOLUTO

INECUACIONES

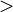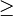En matemática, una inecuación es una desigualdad algebraica en la que aparecen una o más incógnitas en los miembros de la desigualdad.¹ ² Si la desigualdad es del tipo $<$ o $>$ se denomina inecuación en sentido estricto y si es del tipo $\le$ o $\ge$ se denominainecuación en sentido amplio.³

Del mismo modo en que se hace la diferencia entre igualdad y ecuación, una inecuación que es válida para todos las variables se llamainecuación incondicional y las que son válidas solo para algunos valores de las variables se conocen como inecuaciones condicionales.⁴ Los valores que verifican la desigualdad, son sus soluciones.

Inecuaciones

IGUALDADES Y DESIGUALDADES

    Al comparar dos números, b y c, podemos decir que son iguales o desiguales:
                b = c (b es igual a c); b ¹ c (b no es igual a c)
    Si b ¹ c, puede ser: b < c (b menor que c); b > c (b mayor que c).
Ejemplos:
    Para los pares de números (2,2), (7,3), (-2,5) (-6, -3) tendremos:

2=2 son iguales;
7¹ 3 son desiguales 7>3;
-2¹ 5 son desiguales –2<5;
-6¹ -3 son desiguales –6<-3.

En algunas expresiones aparecen los símbolos £ (menor o igual que) o ³ (mayor o igual que).

INECUACIONES

Una inecuación es una desigualdad en la que aparece alguna incógnita en uno de sus miembros o en los dos. Resolver una inecuación es hallar los valores de la incógnita para los que se satisface la desigualdad. Si existe solución, se denomina conjunto solución.

INTERVALOS

Para expresar las soluciones de las inecuaciones es conveniente recordar los distintos tipos de intervalos en la recta real R:

[a, b] = {x: a£ x£ b} intervalo cerrado, x=a y x=b están incluidos;
(a,b) = {x: a<x<b} intervalo cerrado, x=a y x=b no están incluidos;
[a, + ¥ ) = {x: x³ a} intervalo al infinito, x=a está incluido;
(a, + ¥ ) = {x: x>a} intervalo al infinito, x=a no está incluido;
(- ¥ ,b) = {x: x<b} intervalo al infinito, x=b no está incluido;
(- ¥ ,b] = {x: x£ b} intervalo al infinito, x=b está incluido.

INECUACIONES DE PRIMER GRADO CON UNA INCÓGNITA

La resolución de las inecuaciones se realiza aplicando las propiedades de las desigualdades:

Si a los dos miembros de una inecuación se les suma (o resta) un mismo número o expresión, la inecuación no varía.
Si se multiplican (o dividen) los dos miembros de una inecuación por un mismo número, distinto de cero, ésta:

-no varía y conserva el sentido si el número es positivo
-no varía pero cambia el sentido si el número es negativo.
Ejemplos:

Resolvemos la inecuación 5x+3>3x+1.

Aplicando a. Sumamos a los dos miembros -3,es decir, pasamos el 3 al segundo miembro; de la misma forma, sumamos –3x a los dos miembros, esto es, pasamos 3x al primer miembro:
5x>3x+1-3; 5x>3x-2; 5x-3x>-2; 2x>-2
Aplicando b. Dividimos los dos miembros entre el número positivo 2, no cambia el sentido:
2x/2 > -2/2 ® x>-1
El conjunto solución pertenece al intervalo (-1, +¥ ).
2x+5 £ 2x-4. Restando 2x a ambos miembros obtenemos 5 £ -4, lo que significa que no tiene solución.

INECUACIONES DE PRIMER GRADO CON DOS INCÓGNITA

Una ecuación lineal con dos incógnitas se puede escribir, una vez simplificada, de las siguientes formas:
y > ax+b; y ³ ax+b; y <ax+b; y £ ax+b.

El conjunto solución viene dado por un semiplano, P+ o P-.
En primer lugar representamos la recta y=ax+b que divide el plano en dos semiplanos.
Los puntos del semiplano situados por encima de la recta presentan la ordenada en el origen mayor que esta, verificándose la inecuación y>ax+b, P+.
Por tanto para los puntos del semiplano P- el valor de la ordenada es menor que la correspondiente de la recta, se cumple y<ax+b.

A CONTINUACION TE PRESENTAMOS EL SIGUIENTE VIDEO DE COMO RESOLVER INECUACIONES

lunes, 14 de enero de 2013

PENDIENTE DE UNA RECTA

En matemáticas y ciencias aplicadas se denomina pendiente a la inclinación de un elemento ideal, natural o constructivo respecto de la horizontal.

En geometría, puede referirse a la pendiente de la ecuación de una recta como caso particular de la tangente a una curva, en cuyo caso representa laderivada de la función en el punto considerado, y es un parámetro relevante, por ejemplo, en el trazado altimétrico de carreteras, vías férreas o canales.

Definición

La pendiente de una recta en un sistema de representación rectangular (de un plano cartesiano ), suele ser representado por la letra $m$ , y es definido como el cambio o una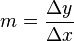

diferencia en el eje Y dividido por el respectivo cambio en el eje X, entre 2 puntos de la recta. En la siguiente ecuación se describe:

toda recta que no sea horizontal, tiene que cortar al eje "x". Se dice que si una recta corta al eje X, la inclinación de la recta se define como el ángulo positivo menor de 180°.

$m = \frac{\Delta y}{\Delta x}$

TIPOS DE PENDIENTES

Pendiente	Tipo de recta
positiva	recta ascendente
negativa	recta descendente
cero	recta horizontal
no definida	recta vertical

Indirecta:

Obtenemos dos puntos (x e y) a partir de dos valores dados a x (por ejemplo, x = 1 y x = 2), y los ponemos en la ecuación de la recta:

3x − y − 4 = 0 si (x = 1)

3(1) − y − 4 = 0

3 − y − 4 = 0

y − 7 = 0

y = 7

P₁ (1, 7) = (x₁, y₁)

3x − y − 4 = 0 si (x = 2)

3(2) − y − 4 = 0

6 − y − 4 = 0

y − 10 = 0

y = 10

P₂ (2, 10) = (x₂, y₂)

Ahora sustituimos en la fórmula de la pendiente:

(esta es la pendiente)

Directa:

Basándonos en los valores de la recta podemos conseguir la pendiente:

3x − y − 4 = 0

Ax − By − C = 0

A = cantidad de x

B = cantidad de y

C = Número cualquiera

Ahora solo sustituimos en la fórmula de la pendiente

(esta es la pendiente)

Grado de inclinación

Dada una recta, gráficamente su pendiente nos da su grado de inclinación

Pendiente positiva

Cuando la recta es creciente (al aumentar los valores de x aumentan los de y), su pendiente es positiva, en la expresión analítica m > 0

Pendiente negativa

Cuando la recta es decreciente (al aumentar los valores de x disminuyen los de y), su pendiente es negativa, en la expresión analítica m < 0

Pendiente nula o cero

Cuando la recta es constante se dice que tiene pendiente nula, en la expresión analítica m = 0

Visualmente, también podemos definir si la pendiente es positiva o negativa:

Si el ángulo que forma la recta con la parte positiva del eje OX es agudo, la pendiente es positiva y crece al crecer el ángulo.

Si el ángulo que forma la recta con la parte positiva del eje OX es obtuso, la pendiente es negativa y decrece al crecer el ángulo.

A CONTINUACION TE PRESENTAMOS EL SIGUIENTE VIDEO DE COMO SACAR LA PENDIENTE DE UNA RECTA

FUNCIONES LINEALES

En geometría y el álgebra elemental, una función lineal es una función polinómica de primer grado; es decir, una función cuya representación en el plano cartesiano es una línea recta. Esta función se puede escribir como:

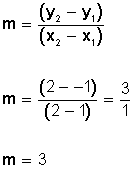
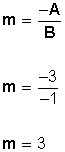
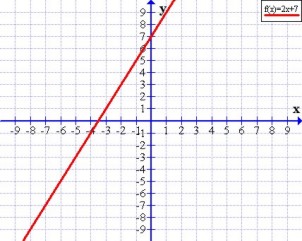
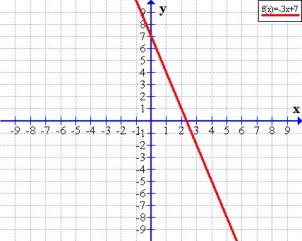
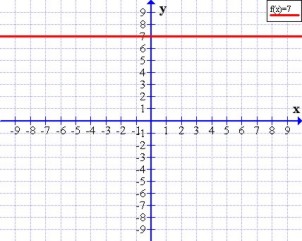
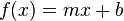
$f(x) = m x + b \,$

donde m y b son constantes reales y x es una variable real. La constante m es la pendiente de la recta, y b es el punto de corte de la recta con el eje y. Si se modifica m entonces se modifica la inclinación de la recta, y si se modifica b, entonces la línea se desplazará hacia arriba o hacia abajo.

Algunos autores llaman función lineal a aquella con b= 0 de la forma:

$f(x) = m x \;$

mientras que llaman función afín a la que tiene la forma:

$f(x) = m x + b \;$

cuando b es distinto de cero.

EJEMPLO

Una función lineal de una única variable dependiente x es de la forma:

$y = m \; x + b \,$

que se conoce burruñis como ecuación de la recta en el plano xy.

En la figura se ven dos rectas, que corresponden a las ecuaciones lineales siguientes:

$y = 0,5\; {x} + 2 \,$

en esta recta el parámetro m= 1/2 por tanto de pendiente 1/2, es decir, cuando aumentamos x en una unidad entonces y aumenta en 1/2 unidad, el valor de bes 2, luego la recta corta el eje y en el punto y= 2.

En la ecuación:

$y = -{x} + 5 \,$

la pendiente de la recta es el parámetro m= -1, es decir, cuando el valor de xaumenta en una unidad, el valor de y disminuye en una unidad; el corte con el eje y es en y= 5, dado que el valor de b= 5.

En una recta el valor de m se corresponde al ángulo $\theta\,$ de inclinación de la recta con el eje de las x a través de la expresión:

$m = \tan \theta \,$

FUNCION LINEALES DE VARIAS VARIABLES

Las funciones lineales de varias variables admiten también interpretaciones geométricas. Así una función lineal de dos variables de la forma

$f(x,y) = a_1 x + a_2 y \,$

representa un plano y una función

$f(x_1,x_2,...,x_n) = a_1 x_1 + a_2 x_2 + ... + a_n x_n \,$

representa una hipersuperficie plana de dimensión n y pasa por el origen de coordenadas en un espacio (n+1)-dimensional.

A CONTINUACION TE PRESENTAMOS EL SIGUIENTE VIDEO DE COMO RESOLVER FUNCIONES LINEALES OBSERVALOS CON ATENCION

Matemáticas