En matemática, una inecuación es una desigualdad algebraica en la que aparecen una o más incógnitas en los miembros de la desigualdad.1 2 Si la desigualdad es del tipo  o
o 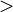 se denomina inecuación en sentido estricto y si es del tipo
se denomina inecuación en sentido estricto y si es del tipo  o
o 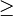 se denominainecuación en sentido amplio.3
Del mismo modo en que se hace la diferencia entre igualdad y ecuación, una inecuación que es válida para todos las variables se llamainecuación incondicional y las que son válidas solo para algunos valores de las variables se conocen como inecuaciones condicionales.4 Los valores que verifican la desigualdad, son sus soluciones.
se denominainecuación en sentido amplio.3
Del mismo modo en que se hace la diferencia entre igualdad y ecuación, una inecuación que es válida para todos las variables se llamainecuación incondicional y las que son válidas solo para algunos valores de las variables se conocen como inecuaciones condicionales.4 Los valores que verifican la desigualdad, son sus soluciones.

 o
o 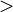 se denomina inecuación en sentido estricto y si es del tipo
se denomina inecuación en sentido estricto y si es del tipo  o
o 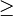 se denominainecuación en sentido amplio.3
se denominainecuación en sentido amplio.3
Inecuaciones
IGUALDADES Y DESIGUALDADES
Al comparar dos números, b y c, podemos decir que son iguales o desiguales:
b = c (b es igual a c); b ¹ c (b no es igual a c)
Si b ¹ c, puede ser: b < c (b menor que c); b > c (b mayor que c).
Ejemplos:
Para los pares de números (2,2), (7,3), (-2,5) (-6, -3) tendremos:
b = c (b es igual a c); b ¹ c (b no es igual a c)
Si b ¹ c, puede ser: b < c (b menor que c); b > c (b mayor que c).
Ejemplos:
Para los pares de números (2,2), (7,3), (-2,5) (-6, -3) tendremos:
2=2 son iguales;
7¹ 3 son desiguales 7>3;
-2¹ 5 son desiguales –2<5;
-6¹ -3 son desiguales –6<-3.
En algunas expresiones aparecen los símbolos £ (menor o igual que) o ³ (mayor o igual que).
INECUACIONES
Una inecuación es una desigualdad en la que aparece alguna incógnita en uno de sus miembros o en los dos. Resolver una inecuación es hallar los valores de la incógnita para los que se satisface la desigualdad. Si existe solución, se denomina conjunto solución.
INTERVALOS
Para expresar las soluciones de las inecuaciones es conveniente recordar los distintos tipos de intervalos en la recta real R:
[a, b] = {x: a£ x£ b} intervalo cerrado, x=a y x=b están incluidos;
(a,b) = {x: a<x<b} intervalo cerrado, x=a y x=b no están incluidos;
[a, + ¥ ) = {x: x³ a} intervalo al infinito, x=a está incluido;
(a, + ¥ ) = {x: x>a} intervalo al infinito, x=a no está incluido;
(- ¥ ,b) = {x: x<b} intervalo al infinito, x=b no está incluido;
(- ¥ ,b] = {x: x£ b} intervalo al infinito, x=b está incluido.
(a,b) = {x: a<x<b} intervalo cerrado, x=a y x=b no están incluidos;
[a, + ¥ ) = {x: x³ a} intervalo al infinito, x=a está incluido;
(a, + ¥ ) = {x: x>a} intervalo al infinito, x=a no está incluido;
(- ¥ ,b) = {x: x<b} intervalo al infinito, x=b no está incluido;
(- ¥ ,b] = {x: x£ b} intervalo al infinito, x=b está incluido.
INECUACIONES DE PRIMER GRADO CON UNA INCÓGNITA
La resolución de las inecuaciones se realiza aplicando las propiedades de las desigualdades:
- Si a los dos miembros de una inecuación se les suma (o resta) un mismo número o expresión, la inecuación no varía.
- Si se multiplican (o dividen) los dos miembros de una inecuación por un mismo número, distinto de cero, ésta:
-no varía y conserva el sentido si el número es positivo
-no varía pero cambia el sentido si el número es negativo.
Ejemplos:
- Resolvemos la inecuación 5x+3>3x+1.
- Aplicando a. Sumamos a los dos miembros -3,es decir, pasamos el 3 al segundo miembro; de la misma forma, sumamos –3x a los dos miembros, esto es, pasamos 3x al primer miembro:
5x>3x+1-3; 5x>3x-2; 5x-3x>-2; 2x>-2
Aplicando b. Dividimos los dos miembros entre el número positivo 2, no cambia el sentido:
2x/2 > -2/2 ® x>-1
El conjunto solución pertenece al intervalo (-1, +¥ ). - 2x+5 £ 2x-4. Restando 2x a ambos miembros obtenemos 5 £ -4, lo que significa que no tiene solución.
INECUACIONES DE PRIMER GRADO CON DOS INCÓGNITA
Una ecuación lineal con dos incógnitas se puede escribir, una vez simplificada, de las siguientes formas:
y > ax+b; y ³ ax+b; y <ax+b; y £ ax+b.
y > ax+b; y ³ ax+b; y <ax+b; y £ ax+b.
El conjunto solución viene dado por un semiplano, P+ o P-.
En primer lugar representamos la recta y=ax+b que divide el plano en dos semiplanos.
Los puntos del semiplano situados por encima de la recta presentan la ordenada en el origen mayor que esta, verificándose la inecuación y>ax+b, P+.
Por tanto para los puntos del semiplano P- el valor de la ordenada es menor que la correspondiente de la recta, se cumple y<ax+b.
En primer lugar representamos la recta y=ax+b que divide el plano en dos semiplanos.
Los puntos del semiplano situados por encima de la recta presentan la ordenada en el origen mayor que esta, verificándose la inecuación y>ax+b, P+.
Por tanto para los puntos del semiplano P- el valor de la ordenada es menor que la correspondiente de la recta, se cumple y<ax+b.
A CONTINUACION TE PRESENTAMOS EL SIGUIENTE VIDEO DE COMO RESOLVER INECUACIONES
No hay comentarios:
Publicar un comentario