PENDIENTE DE UNA RECTA

En matemáticas y ciencias aplicadas se denomina pendiente a la inclinación de un elemento ideal, natural o constructivo respecto de la horizontal.

En geometría, puede referirse a la pendiente de la ecuación de una recta como caso particular de la tangente a una curva, en cuyo caso representa laderivada de la función en el punto considerado, y es un parámetro relevante, por ejemplo, en el trazado altimétrico de carreteras, vías férreas o canales.

Definición

La pendiente de una recta en un sistema de representación rectangular (de un plano cartesiano ), suele ser representado por la letra , y es definido como el cambio o una

diferencia en el eje Y dividido por el respectivo cambio en el eje X, entre 2 puntos de la recta. En la siguiente ecuación se describe:

toda recta que no sea horizontal, tiene que cortar al eje "x". Se dice que si una recta corta al eje X, la inclinación de la recta se define como el ángulo positivo menor de 180°.

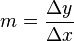
TIPOS DE PENDIENTES

Pendiente	Tipo de recta
positiva	recta ascendente
negativa	recta descendente
cero	recta horizontal
no definida	recta vertical

Indirecta:

Obtenemos dos puntos (x e y) a partir de dos valores dados a x (por ejemplo, x = 1  y  x = 2), y los ponemos en la ecuación de la recta:

3x − y − 4 = 0  si (x = 1)

3(1) − y − 4 = 0

3 − y − 4 = 0

y − 7 = 0

y = 7

P₁ (1, 7) = (x₁, y₁)

3x − y − 4 = 0  si (x = 2) 

3(2) − y − 4 = 0

6 − y − 4 = 0

y − 10 = 0

y = 10

P₂ (2, 10) = (x₂, y₂)

Ahora sustituimos en la fórmula de la pendiente: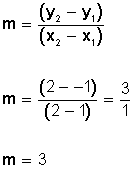

(esta es la pendiente)

Directa:

Basándonos en los valores de la recta podemos conseguir la pendiente:

3x − y − 4 = 0

Ax − By − C = 0

A = cantidad de x

B = cantidad de y

C = Número cualquiera

Ahora solo sustituimos en la fórmula de la pendiente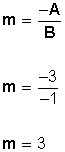

(esta es la pendiente)

Grado de inclinación

Dada una recta, gráficamente su pendiente nos da su grado de inclinación

Pendiente positiva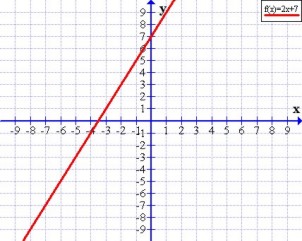

Cuando la recta es creciente (al aumentar los valores de x aumentan los de y), su pendiente es positiva, en la expresión analítica m > 0

Pendiente negativa

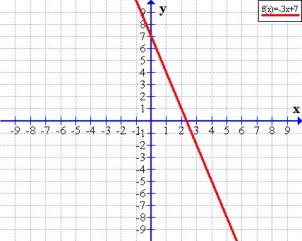Cuando la recta es decreciente (al aumentar los valores de x disminuyen los de y), su pendiente es negativa, en la expresión analítica m < 0

Pendiente nula o cero

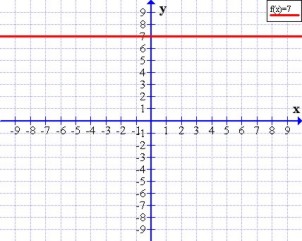Cuando la recta es constante se dice que tiene pendiente nula, en la expresión analítica m = 0

Visualmente, también  podemos definir si la pendiente es positiva o negativa:

Si el ángulo que forma la recta con la parte positiva del eje OX es agudo, la pendiente es positiva y crece al crecer el ángulo.

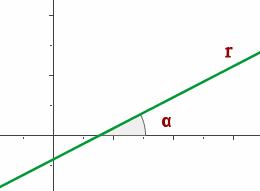Si el ángulo que forma la recta con la parte positiva del eje OX es obtuso, la pendiente es negativa y decrece al crecer el ángulo.

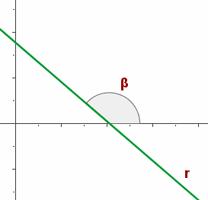A CONTINUACION TE PRESENTAMOS EL SIGUIENTE VIDEO  DE COMO SACAR LA PENDIENTE DE UNA RECTA